Exploring Bar Version Drawing Techniques: A Comprehensive Guide to Picturing Math Concepts
Bar version attracting techniques offer as a useful source for both teachers and trainees in visualizing mathematical concepts. These designs streamline intricate numerical relationships, aiding in the comprehension of addition, reduction, department, and reproduction. This overview outlines effective approaches for carrying out bar models, promoting energetic involvement and real-world links. As visitors discover the functional applications and training ideas, they will uncover how these techniques can change their technique to mathematics.
Comprehending the Basics of Bar Version Drawing
Bar design drawing serves as a powerful visual device in mathematics, facilitating the understanding of problem-solving techniques and mathematical partnerships. This technique entails representing numbers and their relationships through rectangle-shaped bars, making it much easier to imagine procedures such as addition, division, subtraction, and reproduction. Each bar's length corresponds to a certain worth, enabling students to compare amounts and understand proportions clearly.
To develop a bar version, one begins by recognizing the issue's crucial elements, typically damaging it down into components that can be aesthetically represented. For example, in a simple addition trouble, two bars can be drawn, with their sizes standing for the addends. The mixed size shows the amount. In enhancement, bar versions can be adjusted for more complicated troubles, consisting of proportions and portions, by changing the bars as necessary. Mastering these basics lays a strong structure for efficient analytical and deeper mathematical understanding.
Advantages of Using Bar Models in Mathematics
Using bar versions in mathematics provides numerous advantages that boost understanding and understanding. These visual representations help pupils in realizing intricate ideas by damaging them down into convenient components. Bar models offer a clear framework for showing connections in between numbers, making abstract concepts a lot more concrete. They advertise a deeper understanding of mathematical operations and assist in problem-solving by allowing learners to imagine the data they are dealing with.
Bar versions support the development of crucial assuming abilities, as pupils should assess and analyze the visual details to draw verdicts. This technique urges active engagement with the material, strengthening retention and proficiency of mathematical concepts. By promoting a strong structure in aesthetic proficiency, bar models encourage learners to come close to different mathematical difficulties with self-confidence. Overall, the combination of bar models into mathematics education confirms valuable in growing both understanding and logical abilities amongst pupils.
Applying Bar Designs to Addition and Subtraction
Bar versions function as a reliable tool for aesthetically standing for addition and subtraction problems. By highlighting the partnership between numbers, they boost understanding and facilitate analytical. Additionally, real-life applications of these designs can assist students understand mathematical concepts in practical contexts.
Standing For Addition Visually
Aesthetic help can substantially boost their understanding of these operations when trainees come across addition and reduction troubles. Bar designs function as reliable devices for representing addition. By splitting a rectangular shape into segments that represent the numbers included, trainees can envision the partnership in between the amounts. If a student needs to include 3 and 5, they can develop a bar divided right into 2 sections: one section standing for 3 and the various other representing 5. This clear depiction not just streamlines the enhancement process but additionally strengthens the concept of combining amounts. As pupils manipulate these visual aids, they develop a much deeper comprehension of addition, leading to boosted analytical abilities and better confidence in their mathematical capacities.
Reduction With Bar Models
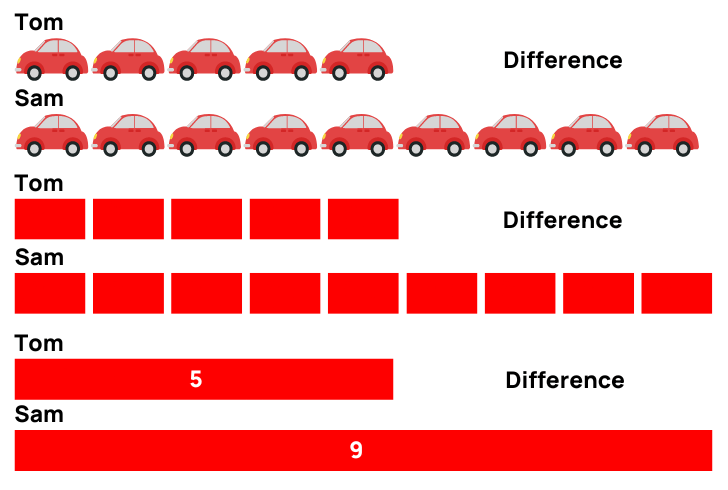
Although reduction is typically perceived as a much more complicated procedure than addition, bar versions can effectively clarify this procedure for pupils. By visually standing for the amounts included, trainees can better understand how numbers associate with one another. In a bar design for reduction, one bar represents the total, while one more shows the amount being subtracted. This aesthetic distinction helps pupils comprehend the principle of "eliminating." If a bar reveals 10 systems, and one more bar standing for 4 units is removed, pupils can conveniently see that 6 devices stay. This strategy not just fosters understanding of subtraction yet also aids in creating analytical skills, enabling trainees to imagine their mathematical reasoning and boost their overall understanding of mathematical principles.
Real-Life Application Examples
Comprehending subtraction with bar versions lays a foundation for using these strategies in real-life circumstances. In various contexts, such as budgeting or buying, people can picture just how much money remains after costs. For circumstances, if a person has $50 and invests $20, a bar version can represent the overall quantity and the spent part, showing that $30 is left. In addition, parents can utilize bar models to help children recognize just how many even more items need to be included to complete a set, such as having three apples and needing five. This visual depiction simplifies intricate problems, helping with comprehension and retention. Inevitably, bar versions work as efficient tools in daily decision-making, boosting mathematical understanding in practical circumstances.
Imagining Multiplication and Division With Bar Models
In discovering the application of bar designs for multiplication and department, it is vital to understand their foundational principles. Constructing reproduction designs permits students to envision relationships in between numbers, while reliable division strategies can be highlighted via these aesthetic help. This strategy enhances comprehension and problem-solving skills in maths.
Comprehending Bar Models
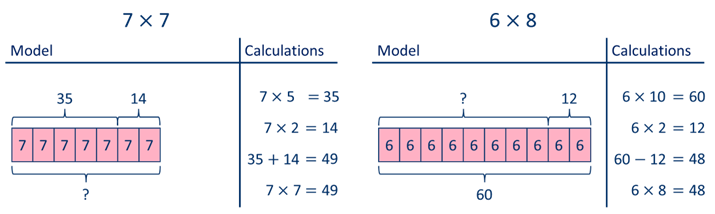
Bar designs act as an effective aesthetic device for illustrating the principles of multiplication and department. They enable students to stand for mathematical relationships in a structured layout, helping with a much deeper understanding of these operations. In multiplication, bar versions show teams of equal size, allowing individuals to imagine the complete quantity when incorporating these teams. Alternatively, in department, bar designs help show exactly how an overall is separated into smaller sized, equivalent components, clarifying the idea of partitioning. By employing these visual aids, trainees can realize the underlying principles of multiplication and department better. This approach not only boosts understanding yet also supports analytic abilities, making bar versions an indispensable property in mathematical education and learning.
Building Multiplication Models
Building multiplication models making use of bar representations offers a clear technique for imagining the process of multiplication. These versions allow students to represent reproduction as teams of equivalent components, making abstract principles more concrete. For circumstances, to illustrate (3 times 4), a student can draw one bar divided into three equal segments, each standing for 4 systems. In addition, developing a second bar with the same length reinforces the understanding of repeated addition, as each sector matches to one team. This graph not only aids in realizing multiplication yet additionally boosts problem-solving skills. By utilizing bar models, trainees can better comprehend relationships in between numbers and establish a robust structure for a lot more intricate mathematical principles, causing increased confidence in their abilities.
Picturing Department Strategies

Fixing Word Problems Using Bar Version Techniques
In a problem involving enhancement and reduction, pupils can attract different bars for each quantity and then control them to locate the service. This process not just makes clear the trouble however also promotes a much deeper theoretical understanding. Bar versions can be adapted for different types of word issues, making them flexible across various mathematical bar model drawing techniques topics. Ultimately, utilizing bar models can greatly enhance trainees' problem-solving skills by offering a clear visual path to come to the correct answer.
Integrating Bar Models in Different Mathematics Topics
Bar designs can be flawlessly integrated into different math topics, boosting students' understanding of concepts past standard math. In algebra, these visual tools help in representing inequalities and formulas, allowing students to picture partnerships in between variables. When tackling geometry, bar versions can highlight the residential or commercial properties of forms and spatial thinking, helping students grasp principles like area and perimeter properly. In stats, bar models assist in the interpretation of information sets, enabling students to compare amounts and identify fads visually. In addition, integrating bar models within measurement subjects aids in comprehending systems and conversions by supplying a tangible representation of quantities. By utilizing bar models across different mathematical locations, educators can foster a much deeper understanding of complex ideas, thus boosting analytical skills and promoting crucial reasoning (bar model drawing techniques). This flexibility demonstrates the utility of bar designs as a foundational tool for trainees in their mathematical trip
Tips for Mentor Bar Designs Properly
Incorporating bar designs right into teaching methods calls for thoughtful approaches to optimize their efficiency. Educators needs to begin by presenting bar models with simple, relatable examples that students can quickly comprehend. This helps to develop self-confidence and knowledge with the principle. Slowly increasing the intricacy of issues permits students to use their skills gradually. In addition, educators need to urge students to develop their own bar designs, promoting active engagement and possession of their discovering.
Integrating joint activities can additionally improve understanding, as trainees go over and solve troubles in groups. Continuous comments is essential; teachers ought to provide positive discourse on trainees' bar model depictions to direct improvement. Attaching bar models to real-life circumstances reinforces their relevance, aiding trainees see the sensible applications of their mathematical skills. By implementing these techniques, educators can successfully harness the power of bar models in their maths guideline.
Often Asked Inquiries
Can Bar Designs Be Made Use Of in Other Topics Besides Math?
Bar designs can without a doubt be utilized in numerous topics past math. They efficiently highlight principles in science, social researches, and language arts, aiding to aesthetically represent relationships, processes, and ideas for boosted understanding across self-controls.
What Age Is Ideal Suited for Knowing Bar Designs?
Bar versions are best suited for children ages 7 to 12, as they develop concrete reasoning skills during this period (bar model drawing techniques). At this age, trainees can properly comprehend abstract ideas through aesthetic representation and analytic strategies
Exist Digital Equipment for Creating Bar Designs?
Exactly How Can I Analyze Pupil Recognizing of Bar Versions?
Evaluating pupil understanding of bar versions can involve tests, observational evaluations, and group conversations. Educators could likewise examine trainees' completed models and their ability to describe their reasoning, making sure a comprehensive examination of comprehension.
What Are Usual Errors When Utilizing Bar Versions?
Usual errors when making use of bar designs consist of misrepresenting amounts, stopping working to precisely identify bars, confusing addition and reduction, neglecting to make use of consistent ranges, and ignoring the importance of clear visual splitting up between different elements.
In enhancement, bar versions can be adjusted for much more complex problems, consisting of ratios and fractions, by changing the bars as necessary. Subtraction is commonly viewed as a much more complicated operation than addition, bar versions can effectively clarify this procedure for pupils. In a bar design for subtraction, one bar represents the total, while an additional shows the quantity being subtracted. If a bar reveals 10 units, and an additional bar standing for 4 units is removed, trainees can quickly see that 6 systems remain. When dividing a total amount right into equivalent groups, students can attract a long bar to represent the entire and then segment it right into smaller bars that suggest each group.